剑指offer - 剪绳子

发表于 | 更新于

题意

给你一根长度为n的绳子，请把绳子剪成m段（n,m均大于1），每段长度记为k[0],k[1],…k[m]。请问k[0]k[1]…k[m]可能的最大乘积是多少。例如绳长为8，剪成三段2,3,3，此时最大乘积是18。

题解

我们考虑第一刀，总共有n-1个位置可以选择，得到的两端绳子长度一共有n-1种。设f(n)为长度为n的绳子剪成m段的最大乘积，假设第一刀剪成i和n-i两端，那么f(n)就等于，f(i)*f(n-i),采用动态规划可以免去重复的多余计算。
需要注意的是，m大于1，也就是说不可以不剪，但是计算f(n)时，我们考虑的是第一刀之后，也就是剪成的两端可以不用再剪。也就是实际上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
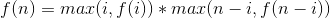
16
class Solution {

public:
    int maxMul(int n){
        int dp[n+1];
        dp[0]=0;
        dp[1]=0;
        for(int l=2;l<=n;l++){
            dp[l]=0;
            for(int i=1;i<=l/2;i++){
                dp[l]=max(max(dp[i],i)*max(dp[l-i],l-i),dp[l]);
            }
        }
        return dp[n];
    }
};