剑指offer - 斐波那契数列

发表于 | 更新于

题目

https://www.nowcoder.com/questionTerminal/c6c7742f5ba7442aada113136ddea0c3

题意

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项。n<=39

题解


递归或迭代均可，递归会进行较多重复计算，迭代更好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int Fibonacci(int n) {
        int a=0,b=1,c;
        if(n==0|n==1) return n;
        while(n-->1)
        {
            c=a+b;
            a=b;
            b=c;
        }
        return c;
    }
};

更炫的写法：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int Fibonacci(int n) {
        int a=0,b=1;
        while(n--)
        {
            b+=a;
            a=b-a;
        }
        return a;
    }
};

扩展题目1

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

题解

跳上n级台阶，最后一步可以跳一级，也可以跳两级，所以f(n)=f(n-1)+f(n-2)。斐波那契数列。

扩展题目2

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

题解

与上题类似，
f(n)=f(n-1)+f(n-2)+……+f(2)+f(1),
f(n-1)=f(n-2)+f(n-3)+……+f(2)+f(1)
所以有
f(n)=f(n-1)*2
f(1)=1
可得到通项公式f(n)=2^(n-1)

扩展题目3

我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

题解

假设最后一个矩形竖着放，共有f(n-1)中方法，假设最后两个横着放，共有f(n-2)种方法。也是斐波那契数列。

思考

上面求斐波那契的方法都是O(N)的，如果我们要求复杂度更小呢？


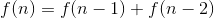
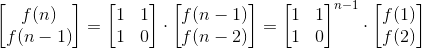
这样我们就可以用矩阵快速幂来求解了。复杂度O(LogN)